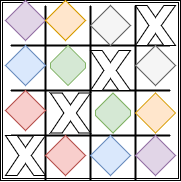
En este ejercicio calcularemos la matriz transpuesta de una matriz 4×4 con respecto a su eje diagonal. Primero rellenaremos con numeros aleatorios del 0 al 9 la primera matriz y despues con la función simétrica calcularemos su transpuesta. conforme al siguiente gráfico. Los elementos de la diagonal marcados con una X permaneceran en el mismo lugar y los elementos que estan en el mismo color son los que se intercambiaran entre si.
package aplicacion1;
/**
*
* @author Javi
*/
public class simetrica {
public static int[][] simetrica(int mat[][]){
int simetric[][];
simetric=new int[4][4];
for (int i=0;i<simetric.length;i++){
for(int j=0;j<simetric[i].length;j++){
simetric[i][j]=mat[3-j][3-i];
System.out.print(simetric[i][j]);
}
System.out.println(" ");
}
return simetric;
}
public static int[][] rellenar(int mat[][]){
for (int i=0;i<mat.length;i++){
for(int j=0;j<mat[i].length;j++){
mat[i][j]=(int)(Math.random()*9);
System.out.print(mat[i][j]);
}
System.out.println(" ");
}
return mat;
}
public static void main(String[] args) {
// TODO code application logic here
int matriz[][];
matriz=new int[4][4];
rellenar(matriz);
System.out.println("matriz simetrica");
simetrica(matriz);
}
}
El resultado sería algo como esto:
0126
1775
2105
8666
matriz simetrica
6556
6072
6171
8210
