Criptografía por transposición
En la guerra del Peloponeso que enfrentó a Espartanos y Atenienses (431 a.C-404 a.C).
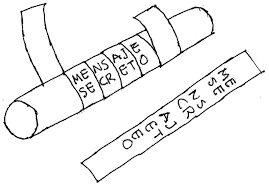
Se usaban cintas para escribir los mensajes, el mensaje se enrrollaba en una escitala o bastón de un grosor determinado, se escribía el mensaje y luego se desenrrollaba la cinta, quedando un texto sin sentido, éste se enviaba y el receptor solo tenía que enrrollar de nuevo la cinta en otra escitala del mismo grosor para descifrar el mensaje.
Este método consiste en transponer los caracteres en el texto cifrado.
Para un texto de n caracteres existe n! posiblidades de ordenación.
Por ejemplo, para un texto de 3 caracteres existirían 3! = 3*2*1 = 6 maneras de organizarlos.
Cifrado César
Con los romanos, continuó la búsqueda de un algoritmo más seguro que el de transposición, empezaron los cifrados de sustitución.
Cada letra del texto original era sustituída por la que le seguía 3 posiciones más adelante, así la A se cifraba con la D, la G con la L…(Téngase en cuenta el alfabeto romano). Posteriormente a todo cifrado en el que la letra original se ha sustituído por otra desplazada un número fijo de posiciones (no necesariamente 3) se denomina: cifrado César.

Este cifrado es vulnerable al criptoanálisis por análisis de frecuencia, a causa del número reducido de claves. Como la sustitución se hace en orden alfabético solo podría haber 21 claves de cifrado diferentes, teniendo en cuenta que el alfabeto romano tiene 21 caracteres. Sin embargo si eliminamos las restricciones de orden alfabético obtenemos 21! =51.090.942.171.709.440.000 posibles claves de cifrado.
Aunque sigue siendo vulnerable al criptoanálisis por análisis de frecuencia.
Cifrados polialfabéticos
En 1460 Leon Battista Alberti propuso un cifrado que consistía en añadir al alfabeto cifrado convencional un segundo alfabeto cifrado.

Así, para cifrar un mensaje se van alternando uno y otro alfabeto por ejemplo, la palabra CASA, la C la cifraríamos con el primer Alfabeto Cifrado quedando una B, la A la cifrariamos con el segundo Alfabeto Cifrado quedando la G, obteniendo de resultado BGRG
En el siglo XVI Vigenère creó el cifrado que se basa en el cuadro de Vigenère, basado en la aportación de Alberti pero en vez de con 2 alfabetos cifrados, con 27 (igual que letras tiene el alfabeto castellano)

El procedimiento sería el mismo que con el cifrado propuesto por Alberti pero utilizando tantos alfabetos cifrados, como letras tenga el alfabeto.






